L’essentiel à retenir : la méthode des moindres carrés minimise la somme des erreurs au carré pour extraire la tendance rationnelle d’un ensemble de données imparfaites. Cette approche transforme le bruit en modèle exploitable, structurant l’incertitude pour mieux anticiper l’avenir. Célèbre pour avoir permis à Gauss de localiser Cérès en 1801, elle demeure l’outil fondamental d’ajustement analytique.
Face à l’incertitude d’un jeu de données apparemment désordonné, comment discerner la tendance de fond sans se laisser égarer par le bruit parasite des mesures ? La méthode des moindres carrés constitue l’outil rationnel indispensable pour tracer une voie juste au milieu de l’imprécision, en réduisant mathématiquement la somme des écarts de votre modèle. Ce guide pratique vous permettra de maîtriser cette technique d’ajustement pour fiabiliser vos analyses, interpréter correctement les résidus et transformer l’imperfection de vos chiffres en une vision claire et exploitable.
- Le principe fondamental : pourquoi minimiser les carrés ?
- La régression linéaire simple : l’application la plus courante
- Au-delà de la ligne droite : les variantes de la méthode
- Les limites et les pièges à éviter
- Applications pratiques et un regard sur les séries temporelles
Le principe fondamental : pourquoi minimiser les carrés ?
L’idée intuitive : trouver le meilleur ajustement possible
Visualisez un nuage de points éparpillés sur un graphique. Votre mission consiste à tracer une ligne droite qui traverse cet ensemble avec le plus de justesse possible. Cette droite incarne votre modèle, c’est-à-dire la meilleure estimation de la tendance générale.
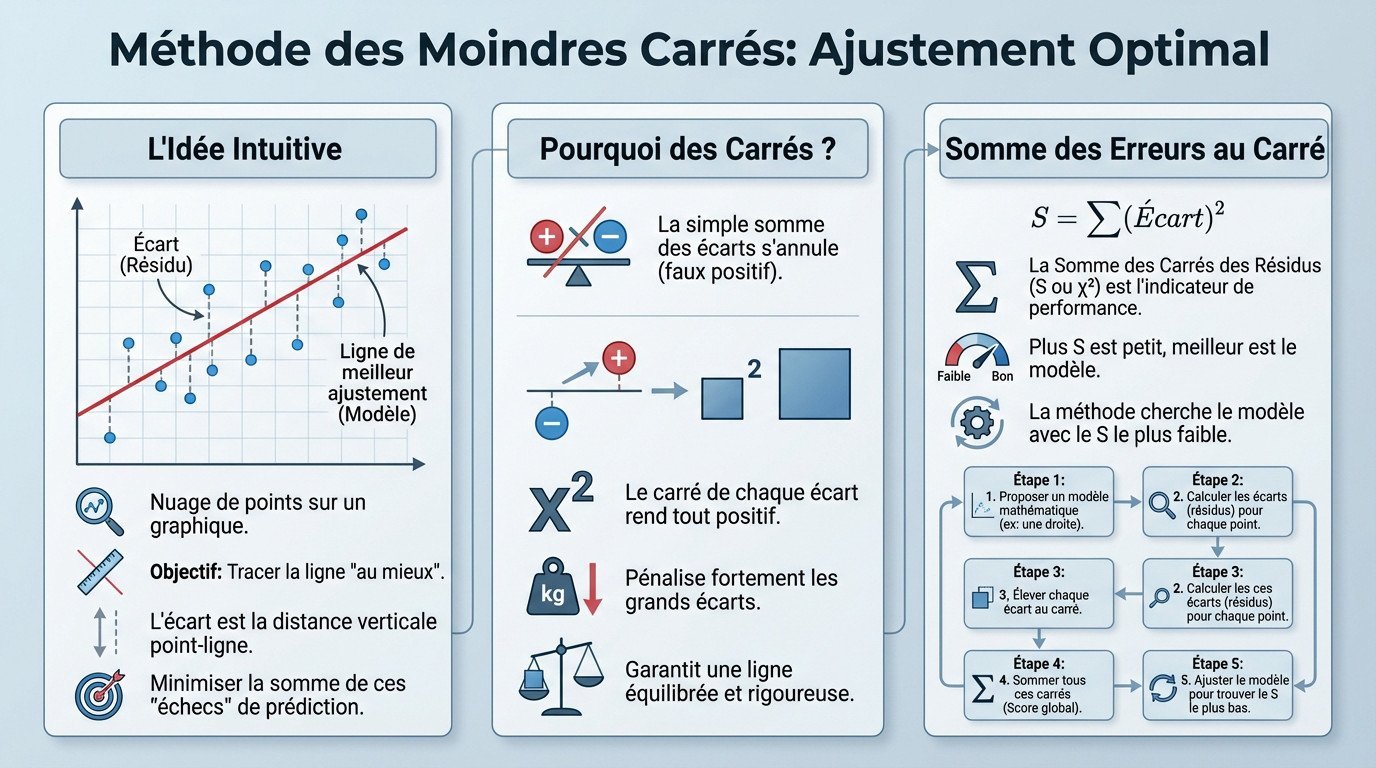
Introduisons ici le concept de résidu. Il s’agit simplement de la distance verticale séparant chaque point réel de votre ligne théorique. Voyez cela comme une petite erreur de prédiction individuelle, un échec localisé propre à chaque donnée.
La methode des moindre carrés vise à réduire au minimum la somme de ces erreurs. C’est l’outil pragmatique pour extraire la vérité la plus probable d’un jeu de données imparfait.
Pourquoi des carrés ? la logique derrière le calcul
Pourquoi ne pas additionner simplement les écarts ? Car les erreurs positives, au-dessus de la ligne, annuleraient les négatives situées en dessous. Ce calcul simpliste donnerait une illusion de perfection totalement trompeuse sur la qualité du modèle.
L’utilisation du carré de chaque écart règle ce souci mathématique. Tout devient positif. Surtout, cela pénalise lourdement les grandes erreurs : un point très éloigné pèse soudainement beaucoup plus dans la balance qu’une petite déviation.
Cette technique force votre ligne à ne négliger aucune donnée excentrée. C’est une approche rigoureuse pour aboutir à un compromis stable, garantissant que le modèle reste fidèle à l’ensemble des observations.
La somme des erreurs au carré : une mesure objective de l’échec
La somme des carrés des résidus (souvent notée S) devient votre unique indicateur de performance. Plus ce chiffre est bas, plus votre modèle est fiable. C’est un score d’échec impartial et mesurable.
Cette méthode n’est donc rien d’autre que la traque systématique du modèle générant le score S le plus faible. C’est un pur problème d’optimisation mathématique pour réduire l’incertitude.
Voici le processus d’exécution pour appliquer cette logique :
- Proposer un modèle mathématique (souvent une droite).
- Calculer les écarts pour chaque point de donnée.
- Élever chaque écart au carré.
- Sommer les carrés pour obtenir l’erreur globale.
- Ajuster le modèle jusqu’à minimiser ce score.
La régression linéaire simple : l’application la plus courante
Modéliser une relation avec l’équation y = ax + b
La régression linéaire reste l’outil de base pour vérifier si deux variables distinctes sont liées. On suppose ici que leur relation peut être approchée par une simple ligne droite. L’équation fondamentale de cette droite est y = ax + b.
Dans cette équation, ‘b’ est l’ordonnée à l’origine, l’endroit précis où la ligne coupe l’axe vertical. ‘a’ est la pente, qui nous dit exactement comment ‘y’ change quand ‘x’ augmente.
Trouver la « meilleure » droite, c’est simplement trouver les meilleures valeurs possibles pour ‘a’ et ‘b’.
Comment la méthode trouve les coefficients optimaux
La méthode des moindres carrés fournit les formules mathématiques pour calculer directement ‘a’ et ‘b’ à partir des données (x, y). Il ne s’agit jamais de tâtonner ou d’estimer au hasard. C’est une solution analytique directe.
Ces formules garantissent que la somme des carrés des écarts entre vos points et la droite sera la plus petite possible. Aucune autre droite ne fera mieux mathématiquement sur ce plan.
Heureusement, vous n’avez pas à faire ces calculs complexes à la main. Des outils comme Excel avec sa fonction DROITEREG ou des logiciels statistiques le font instantanément pour vous.
Un exemple historique : de l’astéroïde Cérès à nos tableurs
L’une des premières applications spectaculaires fut celle du mathématicien Carl Friedrich Gauss en 1801. Il a utilisé cette technique pour prédire la trajectoire de l’astéroïde Cérès à partir de quelques observations seulement. C’était un exploit.
Il a réussi à prédire la trajectoire de la nouvelle planète Cérès là où d’autres avaient échoué lamentablement. Il a prouvé ainsi la puissance et la fiabilité absolue de sa méthode.
La méthode des moindres carrés est un acte de discipline intellectuelle : accepter l’imperfection des données pour en extraire la tendance la plus rationnelle et la plus probable.
Au-delà de la ligne droite : les variantes de la méthode
Mais le monde n’est pas toujours aussi simple qu’une ligne droite parfaite. La methode des moindre carrés a donc dû évoluer pour s’adapter à des situations bien plus complexes.
Quand les données n’ont pas la même fiabilité : les moindres carrés pondérés
Parfois, certaines de vos mesures s’avèrent bien plus précises que d’autres dans votre jeu de données. La méthode de base, dite des Moindres Carrés Ordinaires (MCO), les traite pourtant toutes à une stricte égalité.
Les Moindres Carrés Pondérés (MCP) règlent efficacement ce problème technique. On assigne un « poids » spécifique à chaque point de donnée. Les points les plus fiables, ceux avec une faible incertitude, pèsent alors bien plus lourd dans le calcul.
C’est une façon pragmatique de dire au modèle : « Fais plus confiance à cette donnée-ci qu’à celle-là pour le résultat ».
Gérer les dépendances et les modèles complexes
Que se passe-t-il si les erreurs de vos mesures ne sont pas indépendantes ? C’est souvent le cas avec des données mesurées dans le temps. Les Moindres Carrés Généralisés (MCG) prennent en compte ces corrélations souvent négligées.
Et si la relation n’est pas linéaire du tout (une courbe, par exemple) ? Les moindres carrés non linéaires appliquent le même principe de minimisation des carrés, mais avec des algorithmes plus sophistiqués.
Tableau comparatif des approches
Pour y voir plus clair et choisir l’outil adapté, voici un résumé comparatif des différentes approches.
| Type de méthode | Hypothèse sur l’erreur | Quand l’utiliser ? |
|---|---|---|
| Moindres Carrés Ordinaires (MCO) | Variance constante (homoscédasticité) et erreurs indépendantes. | Le cas de base, quand les données sont « propres » et les mesures de qualité égale. |
| Moindres Carrés Pondérés (MCP) | Variance non constante (hétéroscédasticité). | Quand certaines mesures sont plus précises/fiables que d’autres. On donne plus de poids aux points fiables. |
| Moindres Carrés Généralisés (MCG) | Erreurs corrélées entre elles. | Typique dans les séries temporelles, où l’erreur à un instant T dépend de l’erreur à T-1. |
| Moindres Carrés Robustes | Pas d’hypothèse stricte, tolère les outliers. | Quand le jeu de données est « pollué » par des valeurs aberrantes qui faussent le résultat. |
Les limites et les pièges à éviter
Le talon d’Achille : la sensibilité aux valeurs aberrantes
C’est le danger immédiat de cette approche. Puisque la méthode élève les erreurs au carré, un unique point distant (un outlier) tire brutalement la ligne de régression vers lui et fausse complètement le modèle.
Gardez en tête qu’un seul point aberrant peut significativement modifier l’ajustement global de vos données. Une seule erreur de mesure suffit souvent à tout déséquilibrer.
C’est l’équivalent statistique de laisser une seule émotion extrême dicter toute votre journée. Le résultat final est rarement représentatif de la réalité.
Les hypothèses cachées du modèle
Pour que les résultats soient valides, la methode des moindre carrés s’appuie sur plusieurs suppositions strictes. Si elles ne sont pas respectées, le modèle peut être trompeur.
Un outil n’est utile que si l’on connaît ses conditions d’utilisation. Ignorer les hypothèses d’un modèle, c’est risquer de construire sur du sable.
- Linéarité : La relation entre les variables est bien linéaire.
- Indépendance des erreurs : L’erreur d’une observation n’influence pas celle d’une autre.
- Homoscédasticité : La variance des erreurs est constante.
- Normalité des erreurs : Les erreurs se répartissent selon une loi normale.
Vers des modèles plus résilients
Face au problème récurrent des outliers, des statisticiens ont développé des méthodes robustes. Elles sont conçues pour minimiser l’influence de ces points aberrants sur le résultat final et garantir la stabilité.
Des techniques éprouvées comme les M-estimateurs ou les moindres carrés médians donnent moins de poids aux points extrêmes. Elles cherchent un consensus plus général et solide.
C’est une démarche qui vise à transformer l’adversité en force en ne laissant pas les extrêmes dicter la règle.
Applications pratiques et un regard sur les séries temporelles
Un outil polyvalent : de la finance à l’ingénierie
La méthode des moindres carrés est partout, souvent sans qu’on le sache. C’est un des piliers de l’analyse de données moderne. Elle structure notre compréhension du réel.
Voici quelques domaines où elle s’impose naturellement :
- Finance : pour analyser la performance d’actions ou modéliser des risques.
- Ingénierie : pour l’étalonnage de capteurs ou le traitement du signal.
- Géodésie et Astronomie : pour déterminer des positions et des orbites.
- Économie : pour construire des modèles de prévision.
C’est un des principes essentiels pour réussir à extraire du sens des chiffres au travail. Maîtrisez-le.
L’angle mort : ajuster une tendance dans le temps
Une application intéressante est l’analyse des séries temporelles. On peut utiliser la méthode pour identifier une tendance de fond. Cela s’applique aux données qui évoluent avec le temps. Pensez à vos ventes mensuelles.
Ici, la variable ‘x’ n’est plus une variable indépendante, mais simplement le temps. On regarde jour 1, puis jour 2. On cherche à voir s’il y a une croissance linéaire.
C’est une façon simple de répondre à la question : « Globalement, est-ce que ça monte ou ça descend ?« .
Le piège de l’autocorrélation dans les données temporelles
Attention, appliquer les MCO directement sur des séries temporelles est risqué. Cela viole souvent une hypothèse clé : l’indépendance des erreurs. L’erreur d’aujourd’hui est souvent liée à celle d’hier. Le passé pèse sur le présent.
Ce phénomène s’appelle l’autocorrélation. Si on l’ignore, nos estimations de la fiabilité du modèle seront fausses. Votre analyse perd alors toute sa valeur.
Dans ce cas, il faut se tourner vers des méthodes plus adaptées. Optez pour les MCG ou des modèles spécifiques comme ARIMA. Ces outils prennent ce lien en compte.
Accepter l’imperfection des données pour en extraire une direction claire : voilà l’essence stoïcienne des moindres carrés. Ne cherchez pas la précision absolue, mais la tendance la plus probable. Appliquez cette rigueur mathématique dès aujourd’hui pour objectiver vos analyses.




